반응형
알고리즘 수업시간에 소개받은 문제.
어딘가에서 한번 들어본 적은 있긴 한데... 수업시간에 다시 배우니 아주 새롭다.
1975 년 Steve Selvin 이라는 수학자가 처음 소개한 이래 학자들 사이에서 한동안 많은 논란이 일었던 파라독스 문제라 한다.
문제는 다음과 같다.
당신은 어느 게임쇼에 참가하였다. 이 게임쇼에서는 3 개의 방이 있고 각각의 방 뒤에 임의의 2 곳에는 염소가 있고 나머지 한 곳에는 자동차가 있다. 참가자는 이중 어느 한 방을 선택해서 열어볼 수 있다. 게임쇼의 룰에서는 참가자가 자동차가 있는 문을 선택해서 연다면 이 자동차를 상품으로 받을 수 있고, 염소가 있는 방을 선택해서 연다면 "꽝" 이 된다. 당신이 어떤 방을 열지 결정한 상태에서, 사회자가 당신이 선택하지 않은, 염소가 있는 어느 한 방을 열어서 보여 주면서 당신이 결정한 방을 바꿀 수 있는 기회를 준다고 하자. 이때 처음의 결정을 번복하고 다른 방을 선택하는 것이 좋을까? 아니면 그냥 처음 결정했던 방을 그대로 선택하는 것이 좋을까?
"Suppose you're on a game show, and you're given the choice of three doors: Behind one door is a car; behind the others, goats. You pick a door, say No. 1, and the host, who knows what's behind the doors, opens another door, say No. 3, which has a goat. He then says to you, "Do you want to pick door No. 2?" Is it to your advantage to switch your choice?"
얼핏 생각할 때는 선택을 번복하던 번복하지 않던 별 차이가 없어 보인다. 그래서 이 문제가 소개된 이후 한동안 학자들 사이에서도 논란이 있었단다...
.
.
.
.
.
.
.
.
.
.
답은, 선택을 바꾸어서 다른 방을 열어보는 것이 66% 의 확률로 자동차가 있는 방을 선택할 수 있다. 그 이유는 아래와 같다.
참가자는 1, 2, 3 번과 같이 방을 선택할 수 있다. ( 이 경우 차를 선택할 확률은 33% ) 그가 자신의 결정을 번복하지 않는 다면 어쨌든 차를 선택할 확률은 33.3% 가 될 것이다.
그런데 결정을 번복하는 경우는 아래와 같이 된다.
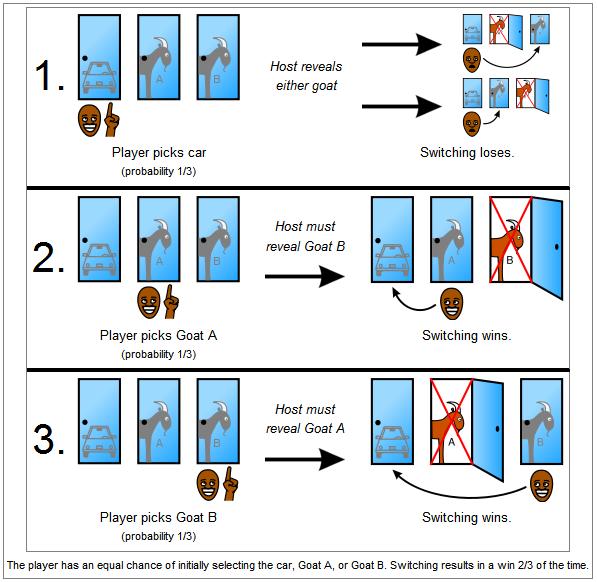
위 그림은 참가자가 처음에 어느 방을 선택했는데, 게임 쇼 진행자가 염소가 있는 방을 보여주었을 때, 선택한 방을 바꾼 경우를 설명하고 있다. 1 번과 같이 처음부터 차가 있는 방을 선택했다면, 선택을 바꿀 경우에는 차를 얻을 수 없다. 반면에 2 와 3 처럼 처음에 염소가 있는 방을 선택했다면, 선택을 바꿀 경우 차를 얻을 수 있다. 결국 선택을 바꿀 경우에는 위의 그림처럼 차를 얻을 확률이 2/3 = 66.6% 가 된다.
교수님의 설명은, 게임 쇼 진행자가 염소가 있는 방을 보여주고, 참가자가 이 것을 본 상태에서 자신의 결정을 번복한 것은 결국 참가자가 방을 두 번 선택한 것과 같은 효과가 있다고 볼 수 있다는 것이다. 그러므로 이 경우 확률은 2/3 이 되는 것이다.
ps ) 이번 학기에 수강중인 "알고리즘 분석" 이란 과목이 있는데... 이제 2 번 들었을 뿐 이지만 아주 대만족이다. 금년에 새로 부임하신 교수님 수업인데... 매 수업시간마다 알고리즘으로 해결 가능한 문제들도 많이 소개를 해 주시고, 각 알고리즘에 대한 증명과 문제점들에 대해서 생각해 보는 시간을 가지면서 명쾌하게 진행하신다. 수강인원도 단 3 명 뿐이라서 거의 개인과외 수준으로 배우는 느낌이다 ㅋㅋ
http://en.wikipedia.org/wiki/Monty_Hall_problem
'Contest > Algorithm' 카테고리의 다른 글
| Java 의 바이너리 서치에는 버그가 있다? (6) | 2010.06.28 |
|---|---|
| "누워서 읽는 알고리즘" 의 퀴즈 정답... (2) | 2010.06.20 |
| 최대공약수(GCD) 와 최소공배수(LCM) (10) | 2008.10.15 |
| 퀵소트(Quick Sort) 의 시간복잡도(Time Complexity) (14) | 2008.09.12 |
| 소수 구하기 (Finding Primes) 알고리즘 (8) | 2008.01.18 |