어떤 자연수 n 이 소수인지 구할때, n 이 작을 경우에는 다음과 같은 방법을 사용한다.
1. Trial Division
소수의 성질을 이용, 어떤 수 n 이 소수인지 판별하기 위해 n 을 2 부터 n-1 까지 하나씩 나누어보아 나누어 떨어지는 수가 존재하지 않으면 n 은 소수가 된다.
Notes
- 2를 제외한 모든 소수는 홀수이므로, 어떤 수 n 이 짝수이면 소수가 아니다.
- 만약 N 이 합성수라면 N = a*b 형태가 되므로 ( a > 1 && b > 1 ), a 와 b 둘 중 하나는 sqrt(N) 보다 작거나 같음을 알 수 있다. 그러므로 N 을 2부터 sqrt(N) 까지 나눠보아 나누어지지 않으면 N 은 소수가 된다.
{
for( int a = 2; a <= end; a++ )
{
if( a%2 == 0 && a != 2 )
{
prime[a] = 0;
continue;
}
for( int b = 2; b*b <= a; b++ )
{
if( a%b == 0 )
{
isprime = false;
break;
}
}
if( isprime ) prime[a] = 1;
}
}
2. 에라토스테네스의 체(Sieve of Eratosthenes)
n 이 작을 때 ( 일반적으로 n <= 10,000,000 ) 2 부터 n 까지의 소수를 찾는 가장 효율적인 방법으로 알려져 있다. 어떤 수 P 가 소수이면 P 로 나눌 수 있는 P 의 배수들은 소수가 아닌 것으로 체크한다. 이러한 과정을 반복하면서 주어진 [2,n] 구간 내에서 소수를 찾아낸다.
{
for( int a = 2; a*a <= end; a++ )
{
if( prime[a] == 0 ) // 'a' is a prime
{
for( int b = a*2; b <= end; b += a )
prime[b] = 1;
}
}
}
소수일 것 같은 수 (Probable Prime) 판별법
어떤 자연수 n 이 소수인지 아닌지 판별할 때, n 이 매우 커지면 유한시간내에 n 이 소수인지 판별하기 곤란해지게 된다. 이 때문에 n 의 소수 여부를 판별하는 근사해를 구하는 검사법이 여럿 개발되었는데, 이 검사법에 의해 n 이 합성수가 아님이 판별되는 경우에 n 을 소수일 것 같다 (Probable Prime) 고 한다.
Probable Prime (PRP) 의 정의는, 소수가 갖는 특정 상태를 만족하는 자연수이다.
1. Wheel Factorization
소수의 특징 중 하나인 [2,n] 구간내에 존재하는 소수의 갯수는 n 이 커질 수록 분포도가 희박해진다는 점에서 착안한 방법. 에라토스테네스의 체의 특수한 응용방법이다. 기본 원리는 에라토스테네스의 체와 동일하나, 구간내의 모든 소수에 대해 배수를 찾아 검사하는 것이 아니라 몇개의 소수를 가지고 이 수들로 나누어지는 수들을 걸러내는 방식으로 구하는 것이 차이점이다. 소수 2, 3을 가지고 Wheel Factorization 을 한다면, 우선 2와 3 의 배수를 모두 소수가 아닌 것으로 판별한다. 그리고 그 다음 소수인 5, 7 를 이용해 또다시 이 작업을 반복한다.
일반적으로 많이 쓰는 factorization 은 6N+1, 6N+5 를 사용하여 주어진 구간 [1,n] 내에서 나누어 지지 않는 수를 소수일 것 같은 수로 판별한다. ( Wheel Factorization 은 n 이 커질수록 정확도가 떨어지므로 이를 위해 n 이 커질수록 더 많은 소수를 이용해 나누어보아야 한다. )
페르마의 마지막 정리로 유명한 수학자 페르마가 제안한 정리.
p 가 a로 나눠지지 않는 소수라면 ap-1 = 1 (mod p) 를 만족해야 한다.
이때 상기 정리를 만족하지 않는 수는 합성수이며, 상기 정리를 만족하는 수는 소수일 가능성이 매우 높은 수(Probable Prime) 가 된다.
증명은 상기 링크 참조.
3. 밀러-라빈 소수판별법 (Miller-Rabin Primality Test)
n 이 소수인지를 검사하려 할 때, 다음 두 식이 성립한다면 a 는 n 이 합성수라는 강한 증거가 된다. ( 이 식이 성립한다면 n 은 소수일 가능성이 매우 높은 수가 된다.)

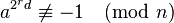 for all
for all 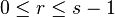
Probable Prime 판별법은 이외에도 여러가지가 개발되어 있다.
참고1
임의의 큰 자연수를 소인수분해하는 문제는 NP 문제로 알려져 있다.
거대한 합성수의 소인수분해는 암호문 해독에 응용되어, 기존의 암호문 전달 체계와 다른 암호학에 공공열쇠 개념을 도입하여 리베스트(Ron Rivest)와, 샤미르(Adi shamir), 아들만(Len Adleman)의 이름을 딴 RSA방식이라는 암호이론이 개발되기도 했다.
http://mathworld.wolfram.com/PrimalityTest.html
참고2 - 관련 사이트
TopCoder Tutorial : Primality Test - Non Deterministic Algorithms
Wikipedia
'Contest > Algorithm' 카테고리의 다른 글
| Java 의 바이너리 서치에는 버그가 있다? (6) | 2010.06.28 |
|---|---|
| "누워서 읽는 알고리즘" 의 퀴즈 정답... (2) | 2010.06.20 |
| Monty Hall Problem (8) | 2009.09.15 |
| 최대공약수(GCD) 와 최소공배수(LCM) (10) | 2008.10.15 |
| 퀵소트(Quick Sort) 의 시간복잡도(Time Complexity) (14) | 2008.09.12 |